Finite-size scaling of survival probability in branching processes

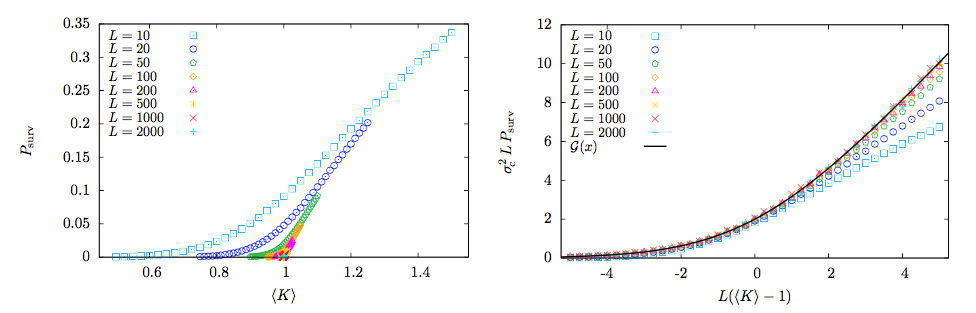
Abstract: Branching processes pervade many models in statistical physics. We investigate the survival probability of a Galton-Watson branching process after a finite number of generations. We derive analytically the existence of finite-size scaling for the survival probability as a function of the control parameter and the maximum number of generations, obtaining the critical exponents as well as the exact scaling function. Our findings are valid for any branching process of the Galton-Watson type, independently of the distribution of the number of offspring, provided its variance is finite. This proves the universal behavior of the finite-size effects in branching processes, including the universality of the metric factors. The direct relation to mean-field percolation is also discussed.