Percolation on trees as a Brownian excursion: from Gaussian to Kolmogorov-Smirnov to exponential statistics

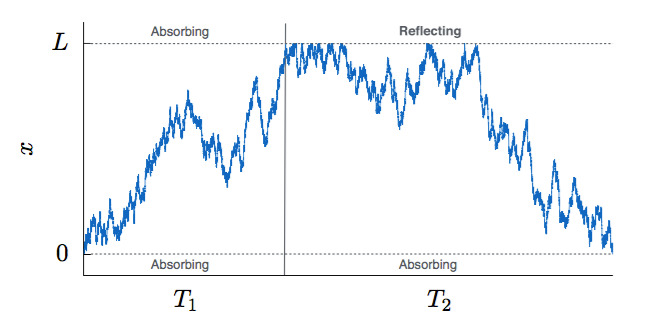
Abstract: We calculate the distribution of the size of the percolating cluster on a tree in the subcritical, critical, and supercritical phase. We do this by exploiting a mapping between continuum trees and Brownian excursions, and arrive at a diffusion equation with suitable boundary conditions. The exact solution to this equation can be conveniently represented as a characteristic function, from which the following distributions are clearly visible: Gaussian (subcritical), Kolmogorov-Smirnov (critical), and exponential (supercritical). In this way we provide an intuitive explanation for the result reported in Botet and Płoszajczak, Phys. Rev. Lett. 95, 185702 (2005) for critical percolation.