Page Not Found
Page not found. Your pixels are in another canvas.
Sitemap
A list of all the posts and pages found on the site. For you robots out there is an XML version available for digesting as well.
Pages
Page not in menu
This is a page not in th emain menu
Posts
Blog Post number 4
Published:
This is a sample blog post. Lorem ipsum I can’t remember the rest of lorem ipsum and don’t have an internet connection right now. Testing testing testing this blog post. Blog posts are cool.
Blog Post number 3
Published:
This is a sample blog post. Lorem ipsum I can’t remember the rest of lorem ipsum and don’t have an internet connection right now. Testing testing testing this blog post. Blog posts are cool.
Blog Post number 2
Published:
This is a sample blog post. Lorem ipsum I can’t remember the rest of lorem ipsum and don’t have an internet connection right now. Testing testing testing this blog post. Blog posts are cool.
Blog Post number 1
Published:
This is a sample blog post. Lorem ipsum I can’t remember the rest of lorem ipsum and don’t have an internet connection right now. Testing testing testing this blog post. Blog posts are cool.
portfolio
Portfolio item number 1
Short description of portfolio item number 1
Portfolio item number 2
Short description of portfolio item number 2
publications
A weighted message-passing algorithm to estimate volume-related properties of random polytopes
Published in Journal of Statistical Mechanics: Theory and Experiment, 2012
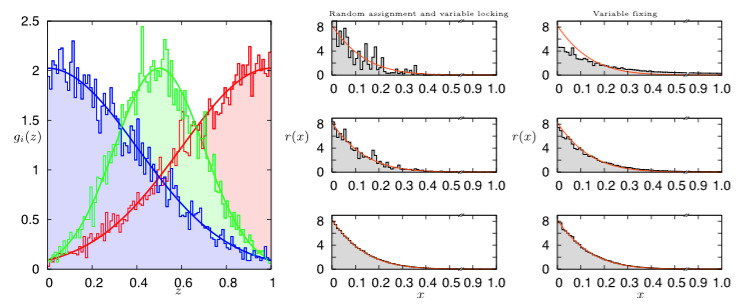
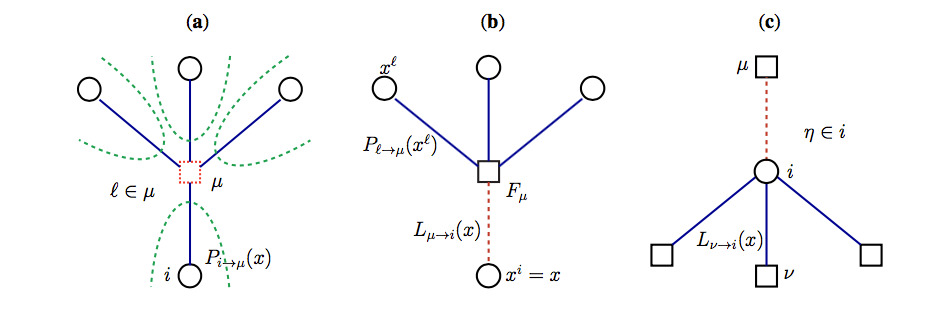
Abstract: In this work we introduce a novel weighted message-passing algorithm based on the cavity method for estimating volume-related properties of random polytopes, properties which are relevant in various research fields ranging from metabolic networks, to neural networks, to compressed sensing. We propose, as opposed to adopting the usual approach consisting in approximating the real-valued cavity marginal distributions by a few parameters, using an algorithm to faithfully represent the entire marginal distribution. We explain various alternatives for implementing the algorithm and benchmarking the theoretical findings by showing concrete applications to random polytopes. The results obtained with our approach are found to be in very good agreement with the estimates produced by the Hit-and-Run algorithm, known to produce uniform sampling.
Download PDF here
A Novel Methodology to Estimate Metabolic Flux Distributions in Constraint-Based Models
Published in Metabolites, 2013
Abstract: Constraint-based metabolic flux analysis describes the space of viable flux configurations for a metabolic network as a high-dimensional polytope defined by the linear constraints that enforce the balancing of production and consumption fluxes for each chemical species in the system. Here we compute the distribution of viable fluxes with a method that scales linearly with system size.
Download PDF here
A scaling law beyond Zipf’s law and its relation to Heaps’ law
Published in New Journal of Physics, 2013
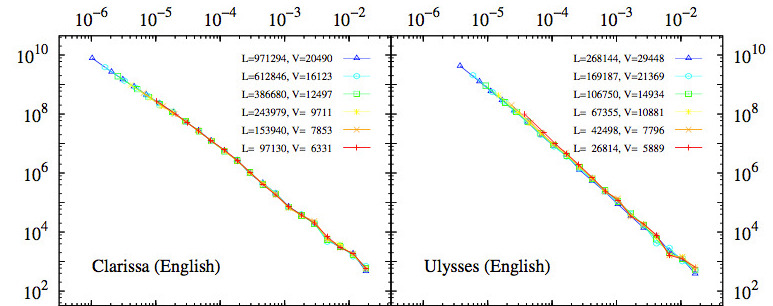
Abstract: The dependence on text length of the statistical properties of word occurrences has long been considered a severe limitation on the usefulness of quantitative linguistics. We propose a simple scaling form for the distribution of absolute word frequencies that brings to light the robustness of this distribution as text grows. In this way, the shape of the distribution is always the same, and it is only a scale parameter that increases (linearly) with text length. By analyzing very long novels we show that this behavior holds both for raw, unlemmatized texts and for lemmatized texts. In the latter case, the distribution of frequencies is well approximated by a double power law, maintaining the Zipf's exponent value γ sime 2 for large frequencies but yielding a smaller exponent in the low-frequency regime. The growth of the distribution with text length allows us to estimate the size of the vocabulary at each step and to propose a generic alternative to Heaps' law, which turns out to be intimately connected to the distribution of frequencies, thanks to its scaling behavior.
Download PDF here
The configuration multi-edge model: Assessing the effect of fixing node strengths on weighted network magnitudes
Published in EPL (Europhysics Letters), 2014
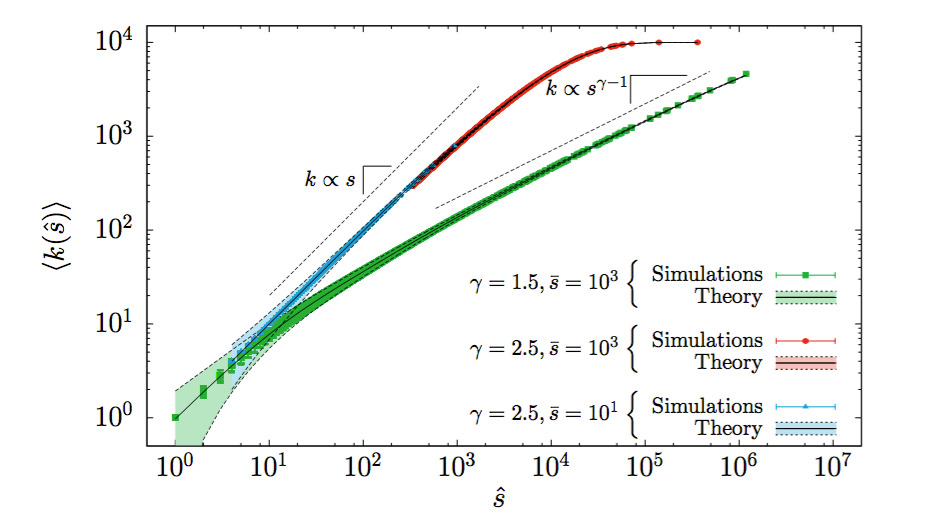
Abstract: Complex networks grow subject to structural constraints which affect their measurable properties. Assessing the effect that such constraints impose on their observables is thus a crucial aspect to be taken into account in their analysis. To this end, we examine the effect of fixing the strength sequence in multi-edge networks on several network observables such as degrees, disparity, average neighbor properties and weight distribution using an ensemble approach. We provide a general method to calculate any desired weighted network metric and we show that several features detected in real data could be explained solely by structural constraints. We thus justify the need of analytical null models to be used as basis to assess the relevance of features found in real data represented in weighted network form.
Download PDF here
Finite-size scaling of survival probability in branching processes
Published in Physical Review E, 2015
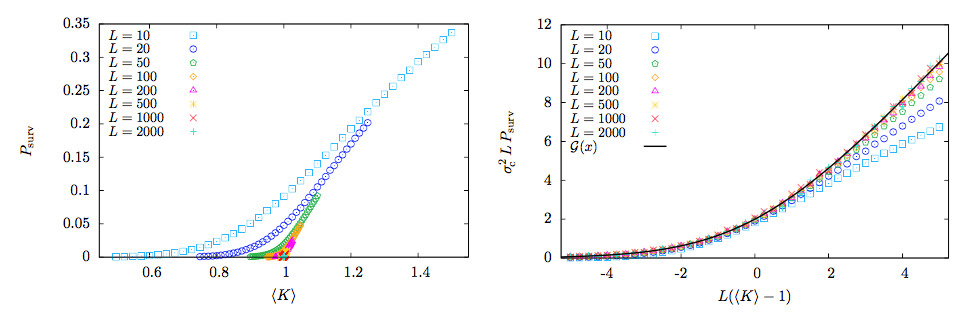
Abstract: Branching processes pervade many models in statistical physics. We investigate the survival probability of a Galton-Watson branching process after a finite number of generations. We derive analytically the existence of finite-size scaling for the survival probability as a function of the control parameter and the maximum number of generations, obtaining the critical exponents as well as the exact scaling function. Our findings are valid for any branching process of the Galton-Watson type, independently of the distribution of the number of offspring, provided its variance is finite. This proves the universal behavior of the finite-size effects in branching processes, including the universality of the metric factors. The direct relation to mean-field percolation is also discussed.
Download PDF here
The perils of thresholding
Published in New Journal of Physics, 2015
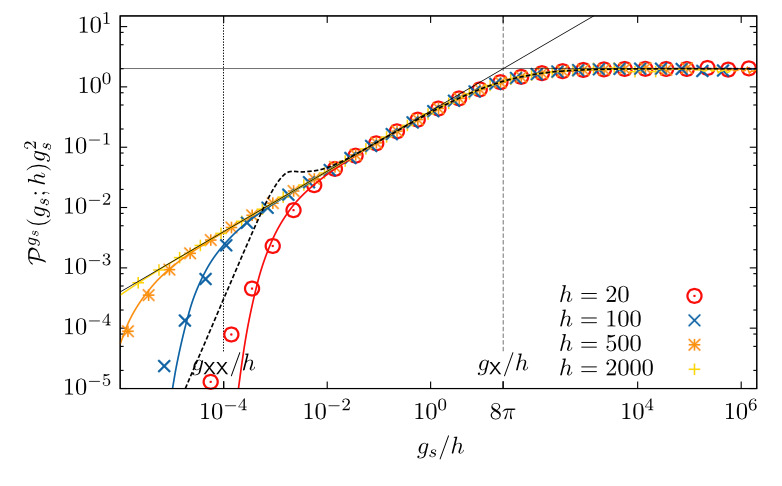
Abstract: The thresholding of time series of activity or intensity is frequently used to define and differentiate events. This is either implicit, for example due to resolution limits, or explicit, in order to filter certain small scale physics from the supposed true asymptotic events. Thresholding the birth–death process, however, introduces a scaling region into the event size distribution, which is characterized by an exponent that is unrelated to the actual asymptote and is rather an artefact of thresholding. As a result, numerical fits of simulation data produce a range of exponents, with the true asymptote visible only in the tail of the distribution. This tail is increasingly difficult to sample as the threshold is increased. In the present case, the exponents and the spurious nature of the scaling region can be determined analytically, thus demonstrating the way in which thresholding conceals the true asymptote. The analysis also suggests a procedure for detecting the influence of the threshold by means of a data collapse involving the threshold-imposed scale.
Download PDF here
Log-log convexity of type-token growth in Zipf’s systems
Published in Physical Review Letters, 2015
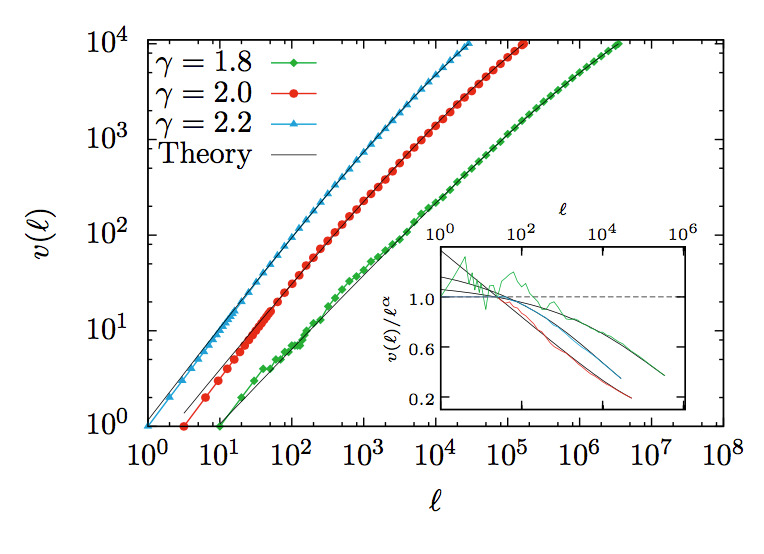
Abstract: It is traditionally assumed that Zipf’s law implies the power-law growth of the number of different elements with the total number of elements in a system—the so-called Heaps’ law. We show that a careful definition of Zipf’s law leads to the violation of Heaps’ law in random systems, with growth curves that have a convex shape in log-log scale. These curves fulfill universal data collapse that only depends on the value of Zipf’s exponent. We observe that real books behave very much in the same way as random systems, despite the presence of burstiness in word occurrence. We advance an explanation for this unexpected correspondence.
Download PDF here
Mapping high-growth phenotypes in the flux space of microbial metabolism
Published in Journal of the Royal Society Interface, 2015
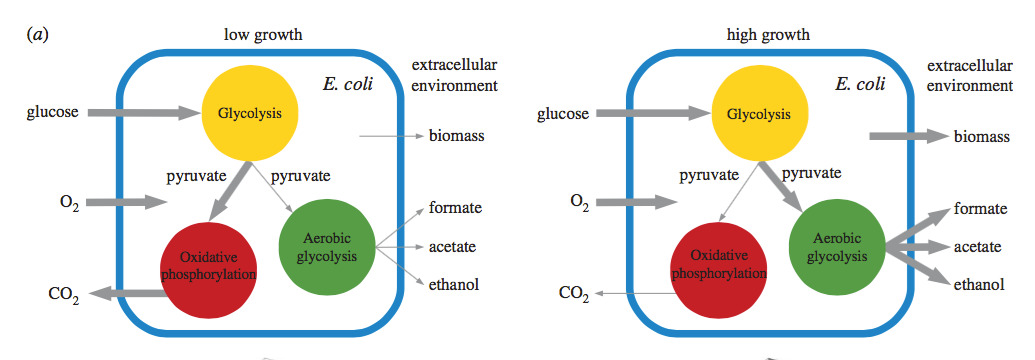
Abstract: Experimental and empirical observations on cell metabolism cannot be understood as a whole without their integration into a consistent systematic framework. However, the characterization of metabolic flux phenotypes is typically reduced to the study of a single optimal state, such as maximum biomass yield that is by far the most common assumption. Here, we confront optimal growth solutions to the whole set of feasible flux phenotypes (FFPs), which provides a benchmark to assess the likelihood of optimal and high-growth states and their agreement with experimental results. In addition, FFP maps are able to uncover metabolic behaviours, such as aerobic fermentation accompanying exponential growth on sugars at nutrient excess conditions, that are unreachable using standard models based on optimality principles. The information content of the full FFP space provides us with a map to explore and evaluate metabolic behaviour and capabilities, and so it opens new avenues for biotechnological and biomedical applications.
Download PDF here
Large-scale analysis of Zipf’s law in English texts
Published in PLOS ONE, 2016
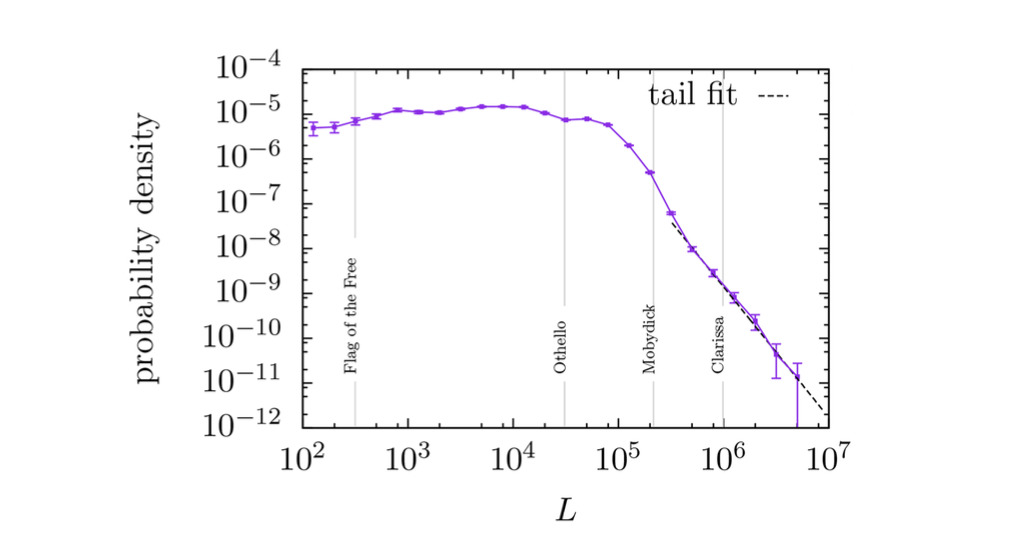
Abstract: Despite being a paradigm of quantitative linguistics, Zipf’s law for words suffers from three main problems: its formulation is ambiguous, its validity has not been tested rigorously from a statistical point of view, and it has not been confronted to a representatively large number of texts. So, we can summarize the current support of Zipf’s law in texts as anecdotic. We try to solve these issues by studying three different versions of Zipf’s law and fitting them to all available English texts in the Project Gutenberg database (consisting of more than 30 000 texts). To do so we use state-of-the art tools in fitting and goodness-of-fit tests, carefully tailored to the peculiarities of text statistics. Remarkably, one of the three versions of Zipf’s law, consisting of a pure power-law form in the complementary cumulative distribution function of word frequencies, is able to fit more than 40% of the texts in the database (at the 0.05 significance level), for the whole domain of frequencies (from 1 to the maximum value), and with only one free parameter (the exponent).
Download PDF here
On the similarity of symbol frequency distributions with heavy tails
Published in Physical Review X, 2016
Abstract: Quantifying the similarity between symbolic sequences is a traditional problem in information theory which requires comparing the frequencies of symbols in different sequences. In numerous modern applications, ranging from DNA over music to texts, the distribution of symbol frequencies is characterized by heavy-tailed distributions (e.g., Zipf’s law). The large number of low-frequency symbols in these distributions poses major difficulties to the estimation of the similarity between sequences; e.g., they hinder an accurate finite-size estimation of entropies. Here, we show analytically how the systematic (bias) and statistical (fluctuations) errors in these estimations depend on the sample size N and on the exponent γ of the heavy-tailed distribution. Our results are valid for the Shannon entropy (α = 1), its corresponding similarity measures (e.g., the Jensen-Shanon divergence), and also for measures based on the generalized entropy of order α. For small α’s, including α = 1, the errors decay slower than the 1/N decay observed in short-tailed distributions. For α larger than a critical value α∗ = 1 + 1 / γ ≤ 2, the 1 / N decay is recovered. We show the practical significance of our results by quantifying the evolution of the English language over the last two centuries using a complete α spectrum of measures. We find that frequent words change more slowly than less frequent words and that α = 2 provides the most robust measure to quantify language change.
Download PDF here
Exact derivation of a finite-size-scaling law and corrections to scaling in the geometric Galton-Watson process
Published in PLOS ONE, 2016
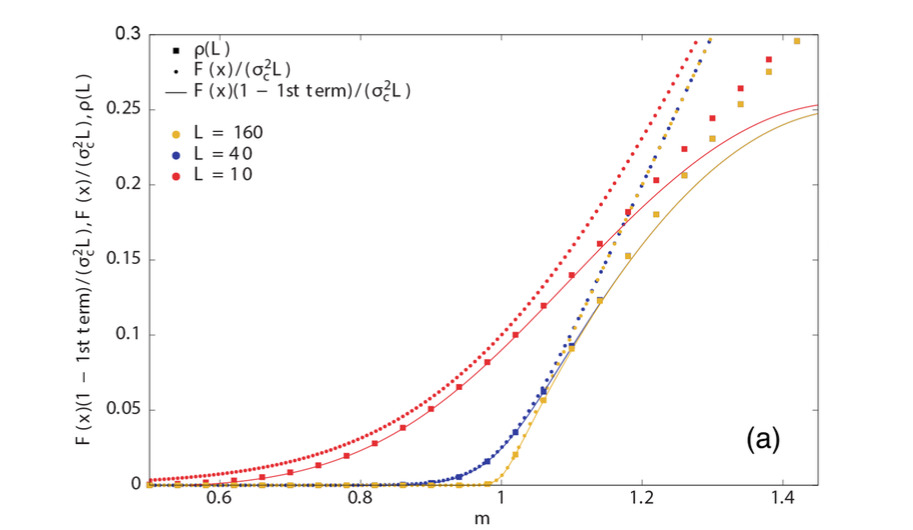
Abstract: The theory of finite-size scaling explains how the singular behavior of thermodynamic quantities in the critical point of a phase transition emerges when the size of the system becomes infinite. Usually, this theory is presented in a phenomenological way. Here, we exactly demonstrate the existence of a finite-size scaling law for the Galton-Watson branching processes when the number of offsprings of each individual follows either a geometric distribution or a generalized geometric distribution. We also derive the corrections to scaling and the limits of validity of the finite-size scaling law away the critical point. A mapping between branching processes and random walks allows us to establish that these results also hold for the latter case, for which the order parameter turns out to be the probability of hitting a distant boundary.
Download PDF here
Percolation on trees as a Brownian excursion: from Gaussian to Kolmogorov-Smirnov to exponential statistics
Published in Physical Review E, 2016
Abstract: We calculate the distribution of the size of the percolating cluster on a tree in the subcritical, critical, and supercritical phase. We do this by exploiting a mapping between continuum trees and Brownian excursions, and arrive at a diffusion equation with suitable boundary conditions. The exact solution to this equation can be conveniently represented as a characteristic function, from which the following distributions are clearly visible: Gaussian (subcritical), Kolmogorov-Smirnov (critical), and exponential (supercritical). In this way we provide an intuitive explanation for the result reported in Botet and Płoszajczak, Phys. Rev. Lett. 95, 185702 (2005) for critical percolation.
Download PDF here
Probing spermiogenesis: a digital strategy for mouse acrosome classification
Published in Scientific Reports, 2017
Abstract: Classification of morphological features in biological samples is usually performed by a trained eye but the increasing amount of available digital images calls for semi-automatic classification techniques. Here we explore this possibility in the context of acrosome morphological analysis during spermiogenesis. Our method combines feature extraction from three dimensional reconstruction of confocal images with principal component analysis and machine learning. The method could be particularly useful in cases where the amount of data does not allow for a direct inspection by trained eye.
Download PDF here
Link to journal
Integrative analysis of pathway deregulation in obesity
Published in npj Systems Biology and Applications, 2017
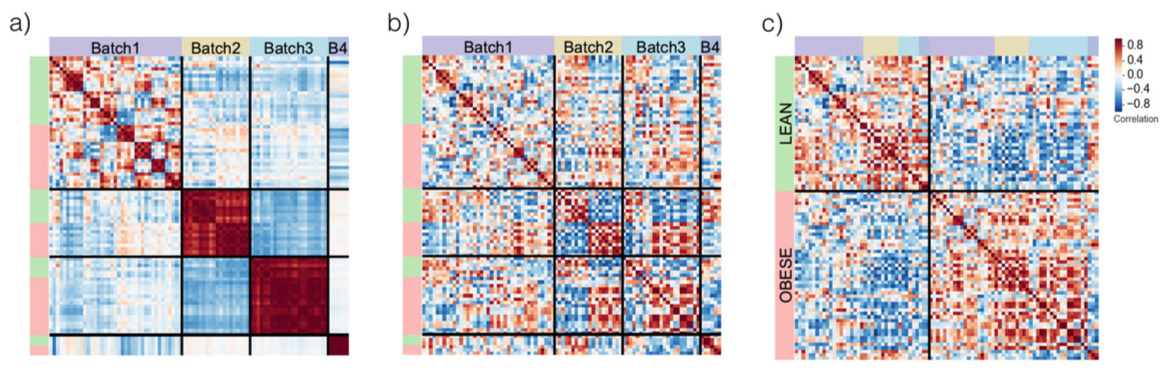
Abstract: Obesity is a pandemic disease, linked to the onset of type 2 diabetes and cancer. Transcriptomic data provides a picture of the alterations in regulatory and metabolic activities associated with obesity, but its interpretation is typically blurred by noise. Here, we solve this problem by collecting publicly available transcriptomic data from adipocytes and removing batch effects using singular value decomposition. In this way we obtain a gene expression signature of 38 genes associated to obesity and identify the main pathways involved. We then show that similar deregulation patterns can be detected in peripheral markers, in type 2 diabetes and in breast cancer. The integration of different data sets combined with the study of pathway deregulation allows us to obtain a more complete picture of gene-expression patterns associated with obesity, breast cancer, and diabetes.
Download PDF here
Link to journal
Dependence of exponents on text length versus finite-size scaling for word-frequency distributions
Published in Physical Review E, 2017
Abstract: Some authors have recently argued that a finite-size scaling law for the text-length dependence of word- frequency distributions cannot be conceptually valid. Here we give solid quantitative evidence for the validity of this scaling law, using both careful statistical tests and analytical arguments based on the generalized central-limit theorem applied to the moments of the distribution (and obtaining a novel derivation of Heaps’ law as a by-product). We also find that the picture of word-frequency distributions with power-law exponents that decrease with text length [X. Yan and P. Minnhagen, Physica A 444, 828 (2016)] does not stand with rigorous statistical analysis. Instead, we show that the distributions are perfectly described by power-law tails with stable exponents, whose values are close to 2, in agreement with the classical Zipf’s law. Some misconceptions about scaling are also clarified.
Download PDF here
Gene expression signature of obesity in monozygotic twins
Published in Physiological Measurement, 2018
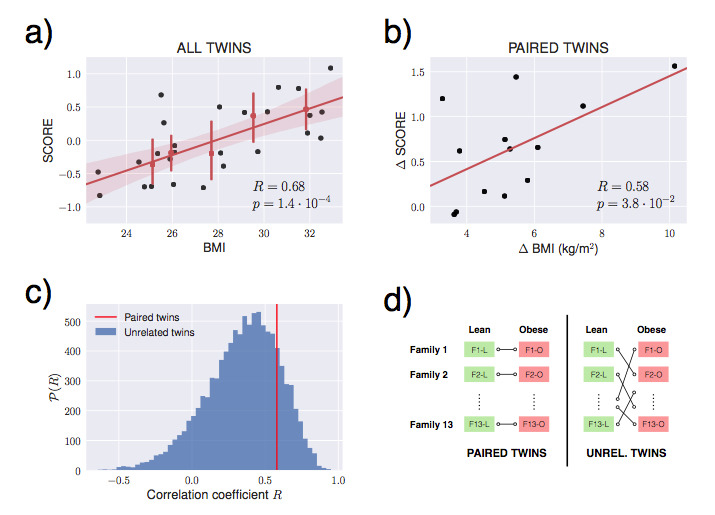
Abstract: Obesity is a disease with a critical increase in childhood. An important unanswered question is to understand if this disease is due to genetic causes or to the life-style of the subjects. To address this question, we have analyzed if monozygotic twins show the same robust transcriptomic signature (5σ, as for the Higgs Boson) that we have recently revealed in obese subjects. Our results show that our signature correlates with BMI in paired transcriptomes of monozygotic twins, suggesting that the signature does not reflect underlying genetic causes.
Download PDF here
Topography of epithelial–mesenchymal plasticity
Published in Proceedings of the National Academy of Sciences, 2018
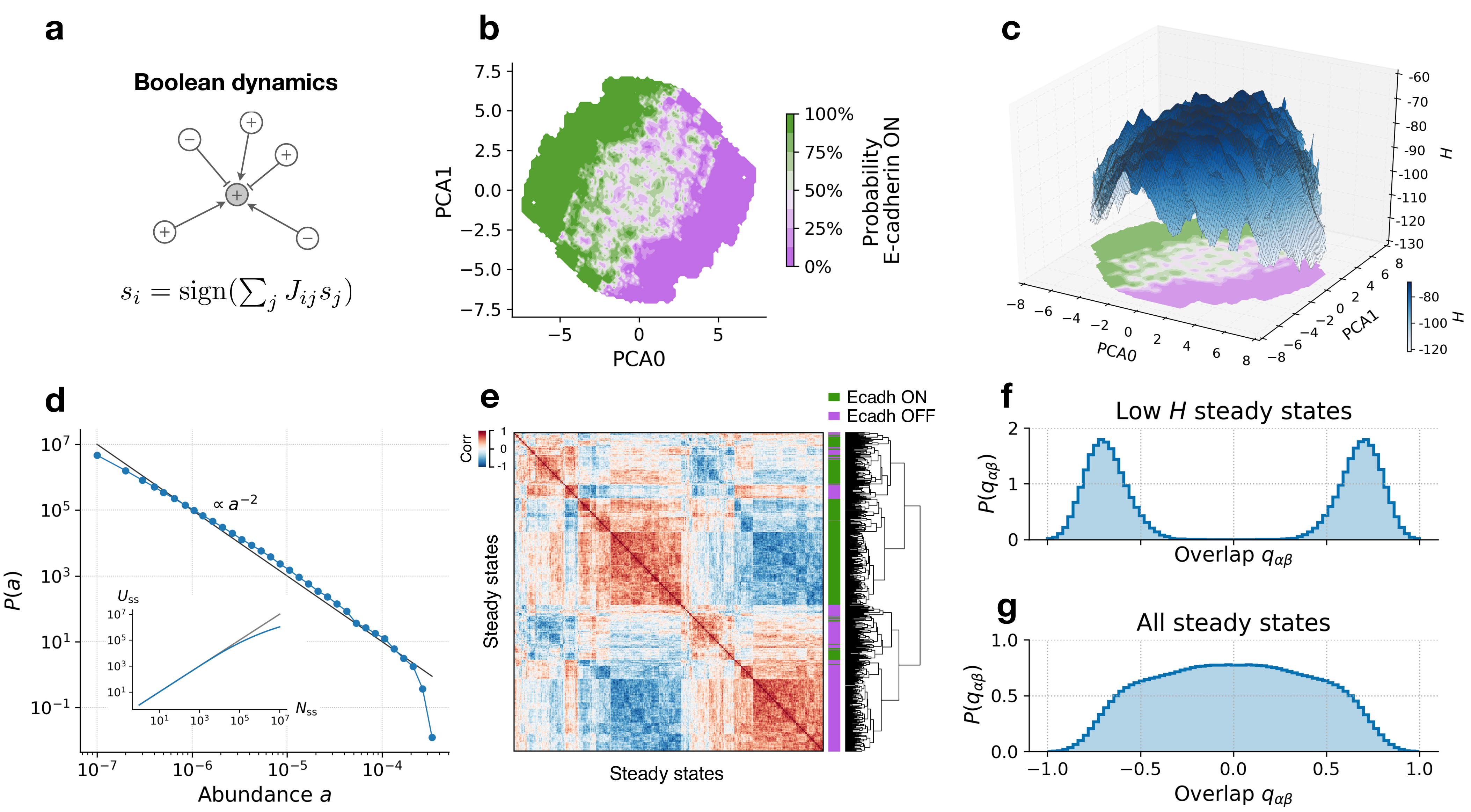
Abstract: The transition between epithelial and mesenchymal states hasfundamental importance for embryonic development, stem cellreprogramming, and cancer progression. Here, we construct atopographic map underlying epithelial–mesenchymal transitionsusing a combination of numerical simulations of a Boolean net-work model and the analysis of bulk and single-cell gene expres-sion data. The map reveals a multitude of metastable hybridphenotypic states, separating stable epithelial and mesenchymalstates, and is reminiscent of the free energy measured in glassymaterials and disordered solids. Our work not only elucidates thenature of hybrid mesenchymal/epithelial states but also providesa general strategy to construct a topographic representation ofphenotypic plasticity from gene expression data using statisticalphysics methods.
Download PDF here
Link to journal
Phase transition, scaling of moments, and order-parameter distributions in Brownian particles and branching processes with finite-size effects
Published in Physical Review E, 2018
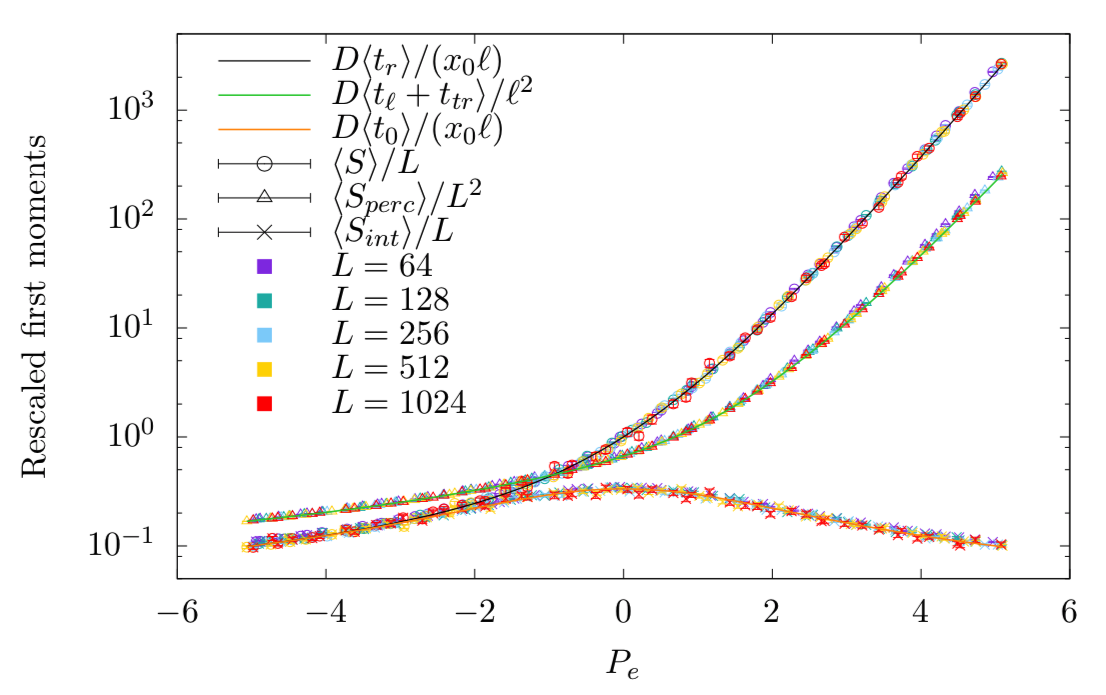
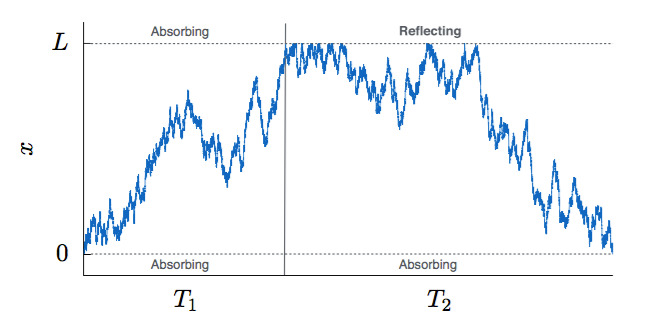
Abstract: We revisit the problem of Brownian diffusion with drift in order to study finite-size effects in the geometricGalton-Watson branching process. This is possible because of an exact mapping between one-dimensional randomwalks and geometric branching processes, known as the Harris walk. In this way, first-passage times of Brownianparticles are equivalent to sizes of trees in the branching process (up to a factor of proportionality). Brownianparticles that reach a distant reflecting boundary correspond to percolating trees, and those that do not correspondto nonpercolating trees. In fact, both systems display a second-order phase transition between “conducting” and“insulating” phases, controlled by the drift velocity in the Brownian system. In the limit of large system size,we obtain exact expressions for the Laplace transforms of the probability distributions and their first and secondmoments. These quantities are also shown to obey finite-size scaling laws.
Download PDF here
A standardized Project Gutenberg corpus for statistical analysis of natural language and quantitative linguistics
Published in Entropy, 2020
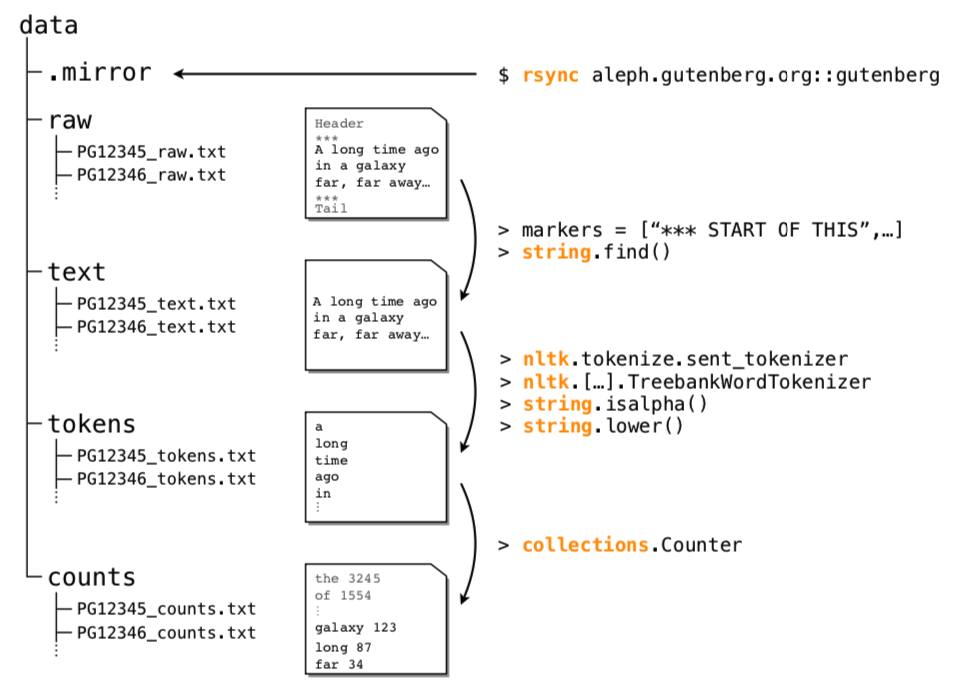
Abstract: We present the Standardized Project Gutenberg Corpus (SPGC), an open science approach to a curated version of the complete PG data containing more than 50,000 books and more than 3 × 10^9 word-tokens. Using different sources of annotated metadata, we not only provide a broad characterization of the content of PG, but also show different examples highlighting the potential of SPGC for investigating language variability across time, subjects, and authors. We publish our methodology in detail, the code to download and process the data, as well as the obtained corpus itself.
Download PDF here
Chromatin and cytoskeletal tethering determine nuclear morphology in progerin expressing cells
Published in Biophysical journal, 2020
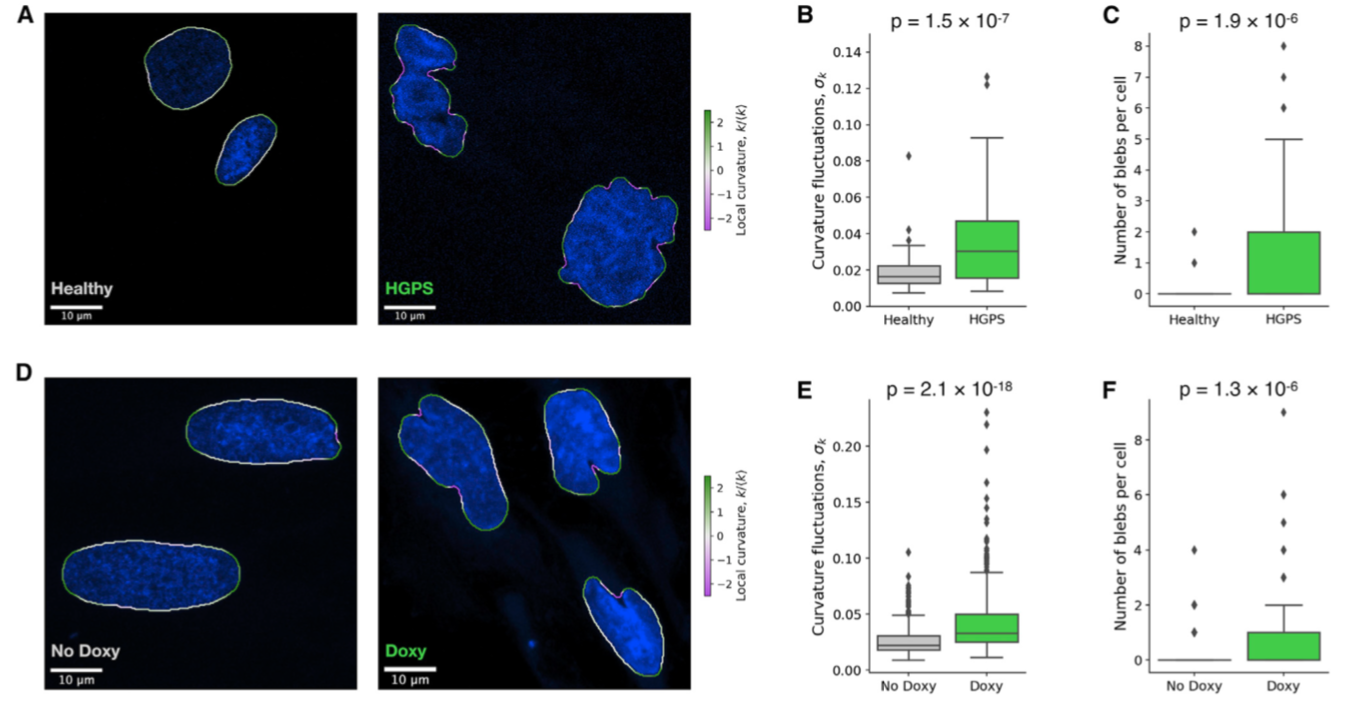
Abstract: Nuclear alterations are often associated with pathological conditions as in Hutchinson-Gilford progeria syndrome, in which a mutation in the lamin A gene yields an altered form of the protein, named progerin, and an aberrant nuclear shape. Here, we introduce an inducible cellular model of Hutchinson-Gilford progeria syndrome in HeLa cells in which increased progerin expression leads to alterations in the coupling of the lamin shell with cytoskeletal or chromatin tethers as well as with polycomb group proteins. Furthermore, our experiments show that progerin expression leads to enhanced nuclear shape fluctuations in response to cytoskeletal activity. To interpret the experimental results, we introduce a computational model of the cell nucleus that explicitly includes chromatin fibers, the nuclear shell, and coupling with the cytoskeleton. The model allows us to investigate how the geometrical organization of the chromatin-lamin tether affects nuclear morphology and shape fluctuations.
Download PDF here
Blood flow contributions to cancer metastasis
Published in iScience, 2020
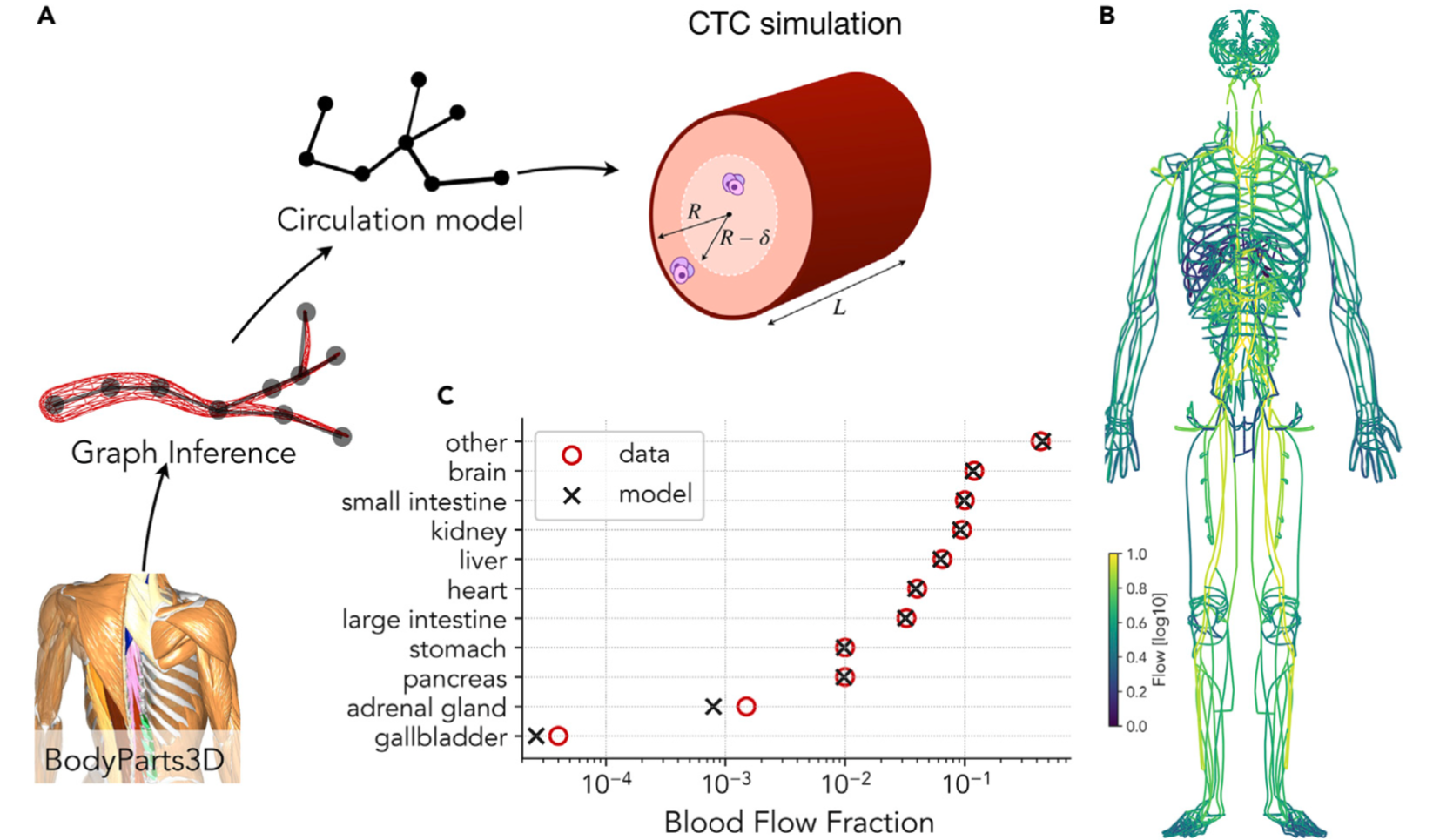
Abstract: The distribution patterns of cancer metastasis depend on a sequence of steps involving adhesion molecules and on mechanical and geometrical effects related to blood circulation, but how much each of these two aspects contributes to the metastatic spread of a specific tumor is still unknown. Here we address this question by simulating cancer cell trajectories in a high-resolution humanoid model of global blood circulation, including stochastic adhesion events, and comparing the results with the location of metastasis recorded in thousands of human autopsies for seven different solid tumors, including lung, prostate, pancreatic and colorectal cancers, showing that on average 40% of the variation in the metastatic distribution can be attributed to blood circulation. Our humanoid model of circulating tumor cells allows us to predict the metastatic spread in specific realistic conditions and can therefore guide precise therapeutic interventions to fight metastasis.
Download PDF here
Link to journal
Identifying inhibitors of epithelial-mesenchymal plasticity using a network topology based approach
Published in npj Systems Biology and Applications, 2020
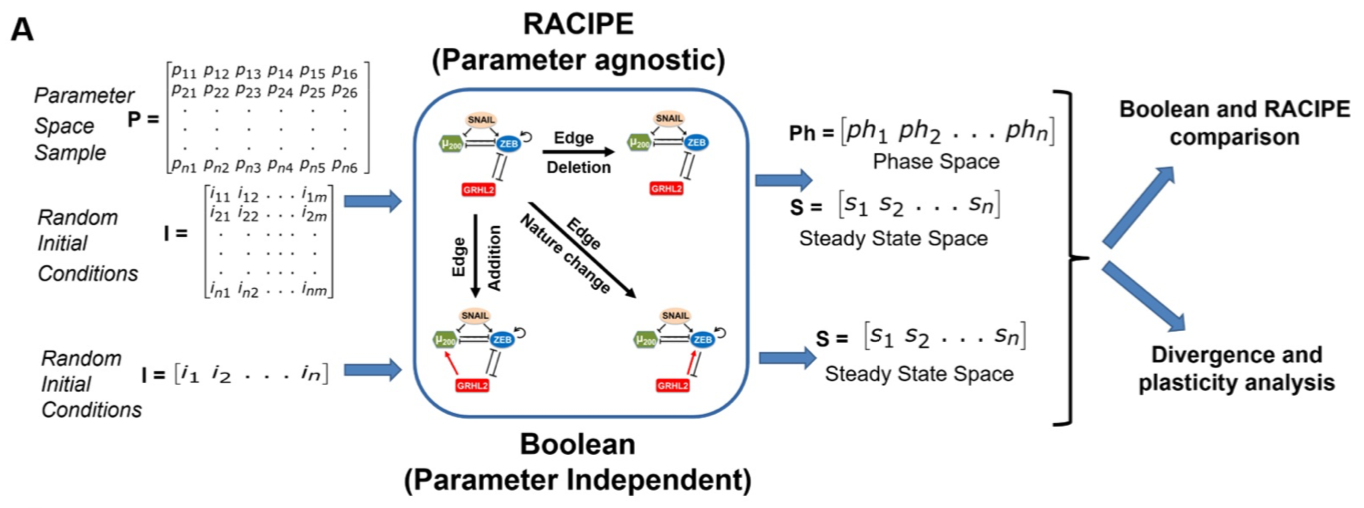
Abstract: We investigate the dynamics of various regulatory networks implicated in Epithelial-Mesenchymal Plasticity (EMP) through two different mathematical modelling frameworks: a discrete, parameter-independent framework (Boolean) and a continuous, parameter-agnostic modelling framework (RACIPE). Results from either framework in terms of phenotypic distributions obtained from a given EMP network are qualitatively similar and suggest that these networks are multi-stable and can give rise to phenotypic plasticity.
Download PDF here
Comparative analysis of metabolic and transcriptomic features of Nothobranchius furzeri
Published in Journal of the Royal Society Interface, 2020
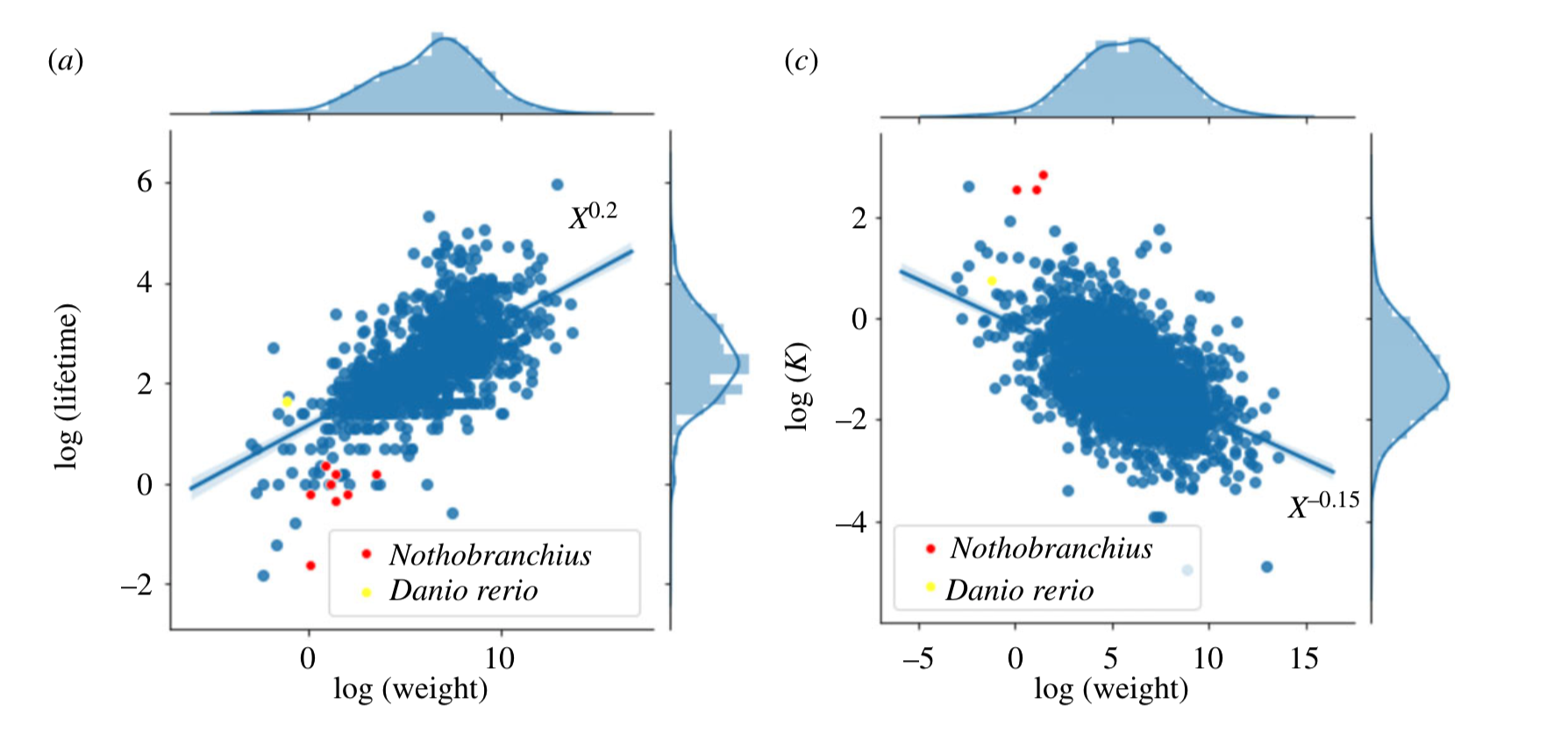
Abstract: Some species have a longer lifespan than others, but usually lifespan is correlated with typical body weight. Here, we study the lifetime evolution of the metabolic behaviour of Nothobranchius furzeri, a killifish with an extremely short lifespan with respect to other fishes, even when taking into account rescaling by body weight. Comparison of the gene expression patterns of N. furzeri with those of zebrafish Danio rerio and mouse (Mus musculus) shows that a broad set of metabolic genes and pathways are affected in N. furzeri during ageing in a way that is consistent with a global deregulation of chromatin. Computational analysis of the glycolysis pathway for the three species highlights a rapid increase in the metabolic activity during the lifetime of N. furzeri with respect to the other species. Our results highlight that the unusually short lifespan of N. furzeri is associated with peculiar patterns in the metabolic activities and in chromatin dynamics.
Download PDF here
Link to journal
MicroRNA-222 regulates melanoma plasticity
Published in Journal of Clinical Medicine, 2020
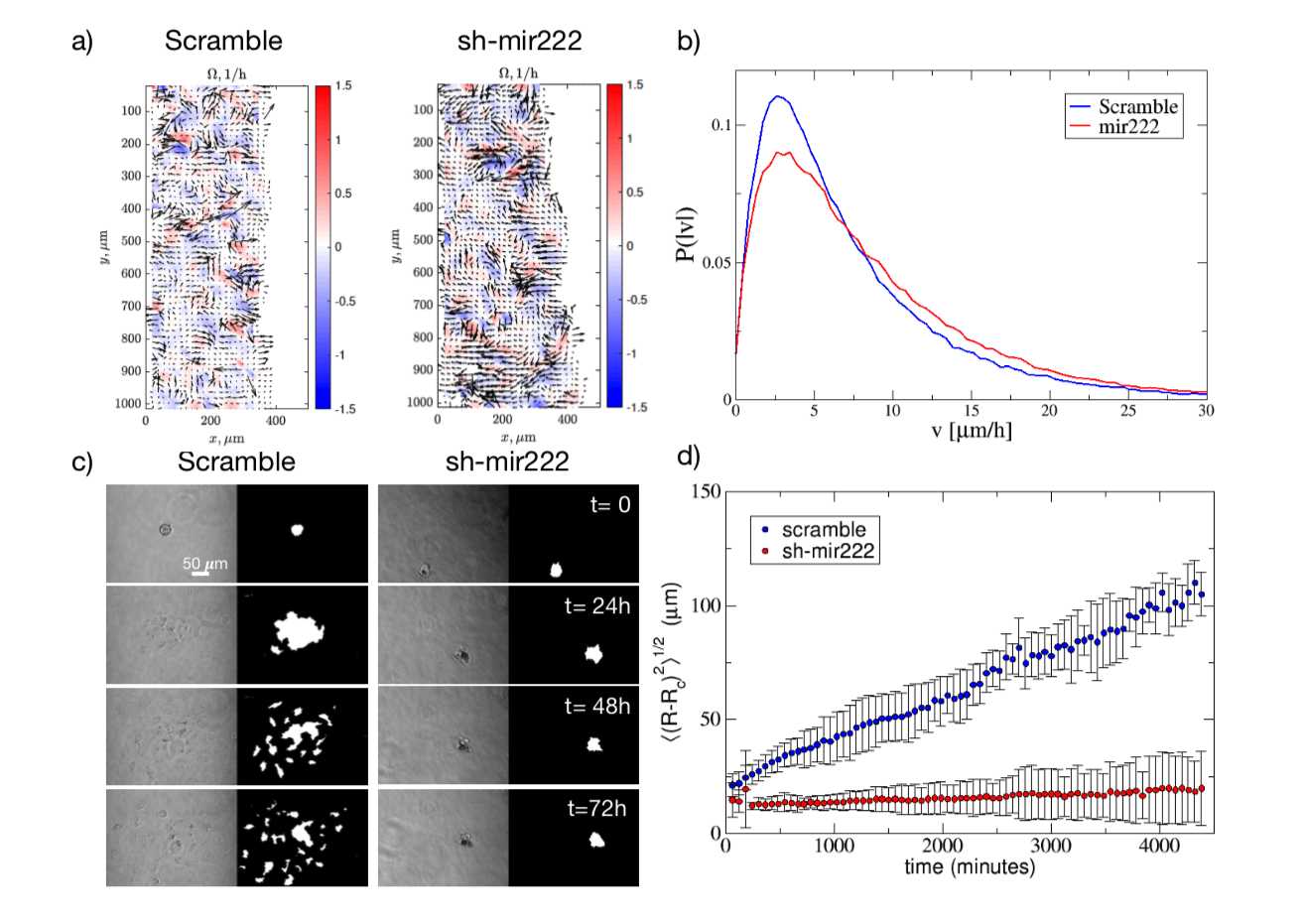
Abstract: Melanoma is one of the most aggressive and highly resistant tumors. Cell plasticity in melanoma is one of the main culprits behind its metastatic capabilities. The detailed molecular mechanisms controlling melanoma plasticity are still not completely understood. Here we combine mathematical models of phenotypic switching with experiments on IgR39 human melanoma cells to identify possible key targets to impair phenotypic switching. Our mathematical model shows that a cancer stem cell subpopulation within the tumor prevents phenotypic switching of the other cancer cells. Experiments reveal that hsa-mir-222 is a key factor enabling this process. Our results shed new light on melanoma plasticity, providing a potential target and guidance for therapeutic studies.
Download PDF here
Link to journal
Automatic design of mechanical metamaterial actuators
Published in Nature Communications, 2020
Abstract: Mechanical metamaterial actuators achieve pre-determined input–output operations exploiting architectural features encoded within a single 3D printed element, thus removing the need for assembling different structural components. Despite the rapid progress in the field, there is still a need for efficient strategies to optimize metamaterial design for a variety of functions. We present a computational method for the automatic design of mechanical metamaterial actuators that combines a reinforced Monte Carlo method with discrete element simulations. 3D printing of selected mechanical metamaterial actuators shows that the machine-generated structures can reach high efficiency, exceeding human-designed structures. We also show that it is possible to design efficient actuators by training a deep neural network which is then able to predict the efficiency from the image of a structure and to identify its functional regions. The elementary actuators devised here can be combined to produce metamaterial machines of arbitrary complexity for countless engineering applications.
Download PDF here
talks
teaching
Teaching experience 1
Published in University 1, Department, 2014
This is a description of a teaching experience. You can use markdown like any other post.
Teaching experience 2
Published in University 1, Department, 2015
This is a description of a teaching experience. You can use markdown like any other post.